LCA(Lowest Common Ancestor) 알고리즘

오늘은 LCA(Lowest Common Ancestor) 알고리즘에 대해 다뤄보겠습니다. 

 

LCA 알고리즘이란? 

제목에서 보시다시피, 최소 공통 조상 알고리즘입니다. 

우선, 아래 그림을 통해 이 알고리즘을 이해해보도록 합시다. 

 

깊이(Depth)란? 

트리

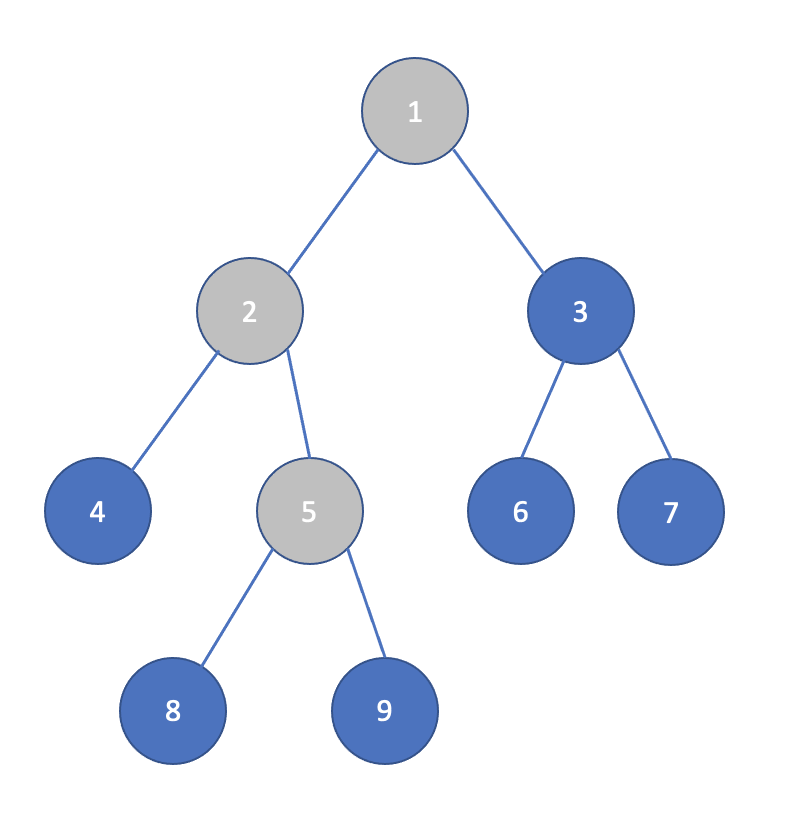
이와 같은 트리가 있다고 할 때, 1이란 값을 가진 Node는 루트(Root)노드라고 불립니다.

루트(Root)노드는 깊이(Depth)가 0이며, 루트를 기준으로 아래부터 1, 2, 3, .. 이런 방식으로 깊이(Depth)가 증가하게 됩니다. 그럼, 노드 9는 깊이가 3, 노드 8의 깊이도 3, 노드 7의 깊이는 2라는 사실을 알 수 있습니다. 

 

조상(Ancestor)이란?

노드 9의 조상(Ancestor)

Depth에 대한 설명을 모두 마쳤으니, 이제 조상(Ancestor)에 대한 이야기를 해보도록 하겠습니다. 

특정 노드의 조상(Ancestor)은 현재 자신과 연결된 부모(Parent) 노드에서 루트(Root) 노드까지 연결된 노드들을 의미합니다. 

즉, 노드 9 조상(Ancestor)은 1, 2, 5 노드가 됩니다. 

 

최소 공통 조상(Lowest Common Ancestor)이란?

앞에서 깊이(Depth)와 조상(Ancestor)이 무엇인지 알아보았는데,

노드 4와 노드 9의 최소 공통 조상(Lowest Common Ancestor)이 무엇일까요? 

 

그림에서 볼 수 있다시피, 노드 2가 (노드 4와 노드 9)의 최소 공통 조상이 됩니다. 

그 이유는 노드 4의 조상은 1, 2 가 되고, 노드 9의 조상은 1, 2, 5 이므로,

공통 조상인 1, 2 중에서 최소(Lowest)인 노드 2가 최소 공통 조상이 되는 것입니다. 

 

그럼, 이제 본격적으로 LCA 알고리즘에 대해 알아봅시다. 

1. DFS (깊이 우선 탐색)을 통해 각 노드의 깊이(Depth)를 계산하고 부모(Parent) 노드를 찾습니다. 

2. 최소 공통 조상을 찾을 두 노드를 입력 받은 경우 (찾을 때 까지 반복)

   2-1. 두 노드의 깊이(Depth)가 같도록 거슬러 올라갑니다. 

   2-2. 두 노드의 깊이(Depth)가 같을 경우, 두 노드의 부모가 같아질 때까지 거슬러 올라가줍니다. 

3. 최소 공통 조상인 노드를 반환 해줍니다. 

 

위 알고리즘을 코드로 구현하면, 아래와 같이 구현할 수 있으며, 시간 복잡도는 O(NM)이 됩니다.

 

 

위에서 배운 내용을 기반으로, 백준(BOJ) 11437 LCA 문제를 풀어보며 익혀보시면 좋습니다. 

https://www.acmicpc.net/problem/11437

11437번: LCA